Surprise! There's Still No Magic Bullet.

As a female student of a physical science, I have a certain amount of interest in the subject of female students in the physical sciences. It turns out we're pretty rare - the gap is practically gone in the biological sciences, closing rapidly in chemistry, and closing slightly more slowly in mathematics, but it's remained stubbornly large in physics, engineering, and computer science. It also turns out we underperform compared to our male colleagues both in introductory classes and on standardized tests. The biggest and most influential gap I'm aware of is on the Physics GRE, but we also apparently underperform on the physics SAT II, math SAT, quantitative GRE, and the standardized pre/post-test used in many introductory physics classes called the "Force Concept Inventory."

Every few years, one study or another comes up with great data showing that girls or women do a lot better in math or science classes when certain changes are made. These changes almost invariably correspond to the techniques that just happen to be generally fashionable in the educational community at the time. When the "new math" was in vogue, there were studies showing that it closed the gender gap (it may have, to some extent, by crippling boys and girls equally); "child-led learning" was supposed to do the same; then there were charter schools, smaller class sizes, and recently a proposed return to gender-segregated schools championed by the sorts of people who said that girls would learn math better by counting flower petals instead of solving equations. It's almost enough to make one cynical.

The method in vogue today is something alternately called "active," "interactive," or "collaborative" learning. It's implemented at the grade school level as "think-pair-share"; for adults in college classrooms, a similar technique is used, but the silly terminology is (thankfully!) left out in favor of more age-appropriate phrases like "peer instruction." The general idea is that a significantly larger portion of class time than usual is devoted to various structured collaborative small-group activities, with or without ensuing full-class discussions.

Now, there are all sorts of ad-hoc rationalizations about why this is supposed to be better for female students in general - we're supposedly more collaborative, less competitive, more timid about answering questions in class, and better at coming up with answers if we can verbalize them in small groups first. The fact that male students almost universally also benefit from changes in teaching techniques designed to benefit girls is always ignored. The observation that nearly all students in serious college-level for-majors math and science courses are atypical in some way, and female students are more often than not gender-atypical, is never taken seriously.

Doing my best to lay aside my own reaction to these teaching techniques (I hate it! I hate talking to people when I haven't had a chance to work out a problem on my own! I hate feeling locked in to a solution because someone has already seen it and listened to me explain it! I hate feeling like I'm teaching my classmates when I'm completely and utterly unqualified to do so! I hate feeling responsible for other people's misconceptions!) Anyway...doing my best to lay all that aside and realize that the generalizations made in studies aren't necessarily intended to apply to me personally, I took a serious look at the Harvard study released a while back that showed that the gender gap could be significantly reduced with the introduction of interactive learning techniques. It seems fairly well-done, with a typical narrative for the sort of study that it is: women were worse off than men coming into a calculus-based physics course and the differences were magnified by the end of the course, new teaching technique was adopted, both women and men did better but women did so much better that the gap was erased.

As I sad, this is typical for the sort of study that it is. You could easily substitute any of the myriad of other educational fashions in for "interactive learning techniques" and find a study that produces basically the same results in some field or other in some age group. To the extent that these studies demonstrate anything, it's that when you take decent instructors, give them a new tool in their teaching toolbox, tell them how to use it, and force them to pay more attention to their teaching (because they're using the new tool), their students do better. This may indirectly help to close the gender gap in some cases by lifting all students up to a similar level of understanding - students, including girls, who come in unprepared are more reliant on being "taught" - but the evidence that any gender-equalization effect is really linked to the techniques' catering to sex-stereotyped learning styles is in my opinion weak at best.

So, as you may guess, I was completely unsurprised to discover that a new study, this one from the University of Colorado, failed to show any statistically-significant gender-gap reduction using the same techniques as the Harvard study. Again, all students did better with the new teaching style, but women didn't gain on men as they did at Harvard. In fact, men made greater gains than women.This ought to be shocking; a "feminine" sex-stereotyped program aimed at improving women's learning actually benefits men more than women. But it's barely worthy of mention, and the study authors make sure to appease the sex-stereotypers by noting that women in the classes did in fact perform in accordance with their stereotypes, doing better than men on "collaborative" homework and worse on "competitive and time constrained" exams, achieving overall grades that were on average equal to the men's. Altogether, the results were impressive as a demonstration of the effectiveness of a new teaching style implemented well, but failed to show any implications for gender equality whatsoever.

So there's still no silver bullet; students, including women, who come into a physics class with less preparation will usually leave with a weaker understanding of the material, the Harvard study notwithstanding. It's possible there may have been a confounding variable like class size, instructor availability, or simply the general higher preparation level of the Harvard students as compared to the Colorado students. But the use of some new teaching techniques can be of general benefit to most students. It doesn't make for good headlines - but responsible science, especially in the social sciences, generally doesn't.

Read more!

Meteors over Canada!

Canada is under attack - from space! In the last week, two meteors have landed in Western Canada. The first was in Alberta on November 20th; the second was in British Columbia yesterday, November 27th. I actually think I may have seen that second one myself, though I was not aware of its nature at the time (I'm a good few hundred miles south of the landing point).

One of the really cool things about being alive in the age of the Internet and ubiquitous video recording devices is that whenever something interesting happens, you can almost always count on there being video of it - and that video will end up on Youtube within the day.

So for anyone who haven't yet seen it, here's the video of the Alberta meteor, caught from a police vehicle camera:

Meteors are really cool. They're chunks of space rock that fall to Earth at tremendous speeds, burning up (partially or wholly, depending on size) in the process. It appears we're in the tail end of meteor season in the the Northern hemisphere right now, according to this lovely explanation from NASA:

To understand why sporadic activity is greatest near the beginning of Fall, simply recall the last time you drove through a swarm of insects. (Splat! There goes another bug on the windshield...) Bugs rarely "splat" on the rear window because it's hard for insects to overtake a fast-moving car from behind. They accumulate instead on the front glass, in the direction that the car is moving.

The same holds true for sporadic meteoroids. They usually meet the Earth in a head-on collision from the direction of our planet's orbital motion around the Sun, a direction that astronomers call "the Earth's apex." The region of sky around the apex is our planet's "front windshield." In late September the apex, as seen from northern latitudes, lies 70 degrees above the horizon at dawn -- that's its highest altitude of the year. With the Earth's "front windshield" so favorably placed, sporadic meteors are easy to see. Northern observers usually count twice as many sporadics in September as they do in March, when the apex has a lower declination.

These big meteors are still very rare though. Two big ones, within a week, right near each other...I'll leave it to the American televangelism industry to figure out whether western Canada's being rewarded or punished. Or maybe it's the start of the Apocalypse. Who knows. Me, I just think sky-rocks are pretty.


Read more!

Bad Science and Bad Logic

I wrote an entry a few days ago praising the science reporting in the New York Times. But it seems that for every good pop-science article, there are a dozen bad ones. Take this latest from Discover Magazine as an example.

Science's Alternative to an Intelligent Creator: The Multiverse Theory

Now, I can't speak with authority on whether the scientists quoted in the article are doing bad science (improbable), or whether they're just terrible at communicating their good science (entirely possible), or whether the person who wrote the article simply misrepresented them horribly (most likely in my opinion). But I do know that the article is woefully misleading in both science and logic.

The article discusses the idea of the "multiverse," which is actually an interesting idea to contemplate. It proposes that there are many (possibly an infinite number of) other universes, which may have different physical laws than our own. Some variations of this theory include the proposition that other universes are continually spawning (possibly even from our own, through black holes or other oddities). Now, there are significant and legitimate arguments for the possible existence of a multiverse. The ones described in the article are not among them.

The authors try to tie the multiverse concept to another legitimate scientific idea: that the existence of the universe as we know it is highly improbable. It turns out that if you tweak certain parameters of our fundamental physical laws, life as we know it - along with other elements of the universe as we know it, such as stars, planets, etcetera - could not exist.

In the process, they commit at least two grievous logical errors which not only undermine their argument but could serve to discredit in the minds of the public the real, legitimate scientific theories which they are claiming to promote.

The first sin against logic is basing their argument on a highly-flawed understanding of probability. In essence, the argument is based on the idea that our universe's laws are highly improbable, but would be more probable if there were a bunch more universes out there. This argument is perhaps emotionally compelling, but it is in fact ridiculous.

It is true that when you play a game of chance a lot of times, it is in fact more likely that you will get a specific desired outcome one of the times. If I play the lottery ten million times, it is more likely that I will win one of those times than if I only play it once. This is basic probability, and most people have an intuitive understanding of it.

However (this is a big however), our intuition frequently leads us astray. The fact is that playing the game many times does not increase the odds of getting the specified outcome on any one specific play. Most of us intuitively believe that it does. It's normal, when playing at a slot machine, to think "I've lost so many times, I'm due to win any minute now!" Casinos base their profits on this intuitive misunderstanding. In reality (and casinos' profit margins operate in reality) the odds of winning the next time you play are completely unaltered by the fact that you lost the last 50 times you played.

This seems contradictory - doesn't playing more increase my chances of winning? Yes. But it doesn't increase my chances of winning at any one particular time. The converse is that knowing I've won on one particular play does not increase the probability that I've played a bunch of other times and lost. If I went out tomorrow, bought a lottery ticket, and won, you would not be able to reason from that outcome that I'd probably played the lottery hundreds or thousands or millions of other times.

How does this relate to the Discover article? The fact is that (assuming the laws of the universe arose by chance and not by some mechanism of necessity that we have yet to discover) all we know is that we've played the game at least once and won. We won this one specific time, and this specific universe has stars and planets and galaxies and life in it. If we had not won, we would not be here to argue about it, so it's guaranteed that in any universe where we exist to talk about it, we won. We can not deduce from that outcome how many times the game was played. It could have been played once, ten times, a thousand times, a million times, an infinite number of times, and none of those would alter the probability of this particular specific universe being the winning ticket. The probability of us being here, in this universe, right now, would be completely unchanged and would remain (again, assuming the laws we're talking about are a matter of chance) statistically infinitesmally small.

The second is invoking a false dichotomy. Here's the claim in the article:

Call it a fluke, a mystery, a miracle. Or call it the biggest problem in physics. Short of invoking a benevolent creator, many physicists see only one possible explanation: Our universe may be but one of perhaps infinitely many universes in an inconceivably vast multi­verse. Most of those universes are barren, but some, like ours, have conditions suitable for life.

Now, I don't know if they got this from the physicists. I certainly hope not. It lends credibility to two horrible anti-science arguments: first, that scientists are out to disprove the existence of a deity (and will go to any number of ridiculously absurd and illogical lengths to do so); second, that observations about the universe as we know it can be used as scientific evidence to point to the existence of a deity. Both of these arguments are patently false. Scientists in general are not hostile to religion and are not out to disprove it, and the fact that our universe is improbable is not an argument for the existence of an even more improbable entity.

Even barring the argument I made above from the discussion and assuming that the multiverse is actually a legitimate solution to the problem of the improbability of our universe (if it is a problem), this argument is still a false dichotomy.

First of all, for the same reason that intelligent design is not a solution to the problem of complexity, a divine or intelligent creator is not a solution to the problem of improbability. The creator/designer itself would have to be complex, and is certainly improbable - it would have to exist in the first place (how? we'll never know unless we can detect and measure it) and have a very specific set of characteristics in order to have created this specific universe as we know it.

Secondly, there are other possible solutions to the problem of improbability. Maybe there's something inherent to the process by which our universe formed that made its characteristics inevitable. Maybe there's something inherent to the stuff that comprises it. We don't know, and we're trying to find out. There are many potential solutions to this problem, and it is horribly disingenuous to point to two of them (neither of which is actually a solution) and claim that they're the only two.

Discover, I'm extremely disappointed in you.

Read more!

Fun with Math Software

One of the things I occasionally enjoy doing in my spare time, odd though it may sound, is playing with math software to make it create cool visuals. I've had a couple of results I've been particularly happy with, so I thought I'd share them with the world.

The first is an animated graphic of a particular concept in vector calculus. The idea is that you have a curve in space, and at any given point you can define three orthogonal vectors with respect to the curve. The first is tangent to the curve (it points along the curve); the second is the normal vector which points in the direction of greatest curvature; and the third is the binormal which is perpendicular to the first two. In terms of physics concepts, if you think of the space curve as the path along which an object is travelling, the tangent vector is in the direction of its velocity (and tangential acceleration), the normal vector is in the direction of its centripetal acceleration, and the binormal vector is, I suppose, just a convenient normal vector to identify the plane in which the object is travelling at a given instant. In this picture, the green vector is the tangent, blue is the normal, and red is the binormal.



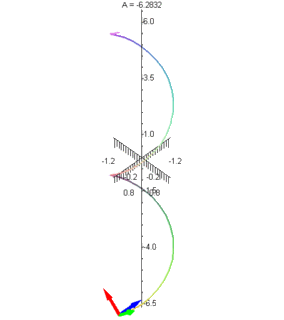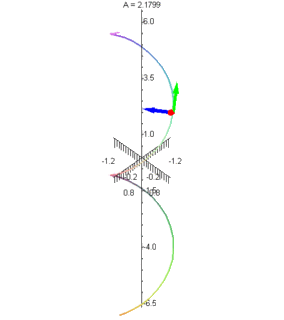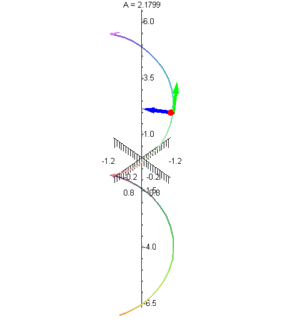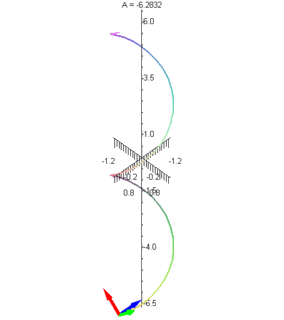
The second animation I have for you is an illustration of what's called a parametric surface. The equation for this surface is rather ugly and complex, but the surface itself is quite beautiful. I have it rotating to give you a complete visual of it. This is an example of math-as-art.


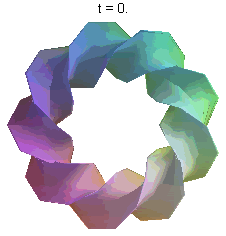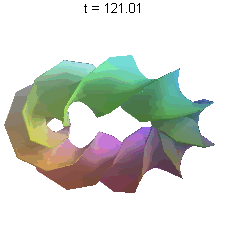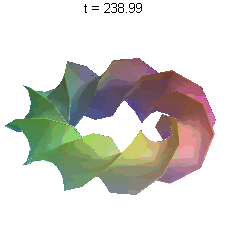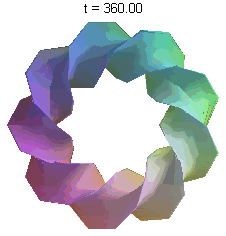
Both of these were done in Maple, which is my personal preferred software for math-art. However, you can do similarly cool things in not only other proprietary software like Mathematica, but also with free (in all senses of the term) software like Maxima, although I don't know the extent to which any free software does animations.

The thing I like most about Maple is that you can talk to it almost entirely in standard math notation, with a few (relatively intuitive) text commands for things like plotting and animating. What I like least about it is that it's a horrendous memory hog and a bit unstable on your standard PC. However, my laptop runs it quite nicely on 64-bit Linux, despite having been entirely incapable of running it under Windows, so it's possible that it may simply have Windows issues.

I rather dislike Mathematica's interface, but there are people who swear by it. As far as Maxima, if you're the sort of person who finds Matlab and command-line Linux easy to deal with, then Maxima is the package for you.

Regardless, however, I do recommend playing with some 3-d graphing-capable software if you're currently a math student (or if you last took math back when slide rules were in vogue); the coolness factor of today's software is really high in the graphics department, and these programs can do some really amazing symbolic math work too.

Read more!

Science Basics: How Theories are Made, Part 2

So you've got your conjecture, and it appears to be consistent with observed reality. The next item on your agenda as a scientist is to decide whether or not your conjecture is within the realm of subjects that can be treated scientifically. There are many subjects that do not fit this description, and you should be aware of them now, before you go to all the trouble of trying to formulate a hypothesis and gather evidence.

Here are the questions you should ask yourself at this stage:

Do I have a solid grasp of the basic science underlying my idea?
Everything in science rests on the fundamental fields of physics, chemistry, and biology. If your exposure to one or more of these fields is limited to high school introductory courses, online reading and pop-science books, it would be an excellent idea to take a full year-long for-majors sequence of introductory courses in that science from a regionally-accredited college or university. It is best to make sure the physics course is calculus based; it is critical to do so if you will be working with physical science ideas. If you can identify the specific fundamental science with which you will primarily be working, it would not be a bad idea to take two different versions of the course, separated in space or time, so that you can be introduced to different viewpoints and ways of understanding the concepts. Most future scientists take an advanced course in their science in high school and then go on to take the introductory sequence at university.

To those who may feel a certain lack of trust in the scientific establishment: Please allow me to assure you that you can trust the content of these introductory courses. The science introduced here is truly fundamental, time-tested and solid. You will work in labs performing experiments to help demonstrate to yourself the validity of the theories presented. However, the entirety of human civilization is effectively a laboratory for these basic theories; these are the aspects of science to which we entrust our lives, our finances, and our precious memories on a daily basis. These are the theories on which airplanes, bridges, heart transplants, compact discs, electrical power systems, blood transfusions, antibiotics, computers, and food crops are built.

To young people and those without access to college courses: You can, of course, do some science without any formal education whatsoever. There are still a few unresolved questions of the sort that can be understood and worked with by high school students and interested laypersons, and there are any number of existing theories that could use some more experimental validation. And a great deal of the science involved in many interdisciplinary fields can be understood fairly well through dedicated self-study, provided that you have the capacity to read and understand introductory-level science textbooks. However, popular science books and the Internet will not provide an adequate background; you will need to seek out and work through books intended for students in the field.

Do I have a solid grasp of the basic mathematics used in science?
There are three basic types of mathematics used in science: algebra, calculus and statistics. The extent to which each of these is used, and the extent to which other types of math may be involved, depends on the specific variety of science. However, you will not be able to escape the need for math entirely. The math required for your introductory science courses or that which you find yourself needing to learn for your self-study program should be largely sufficient, with one exception: you will need to know some statistics to work with experimental data (yours or anyone else's).

Does my idea still fit with what I know about the world?
Now that you know some basic science and math, come back to your original idea. Is it still consistent with what you know about observed reality? If not, you may want to go back to the beginning and build a new conjecture, or you may want to refine your existing one so that it is consistent and possible. This is a personal decision that depends on the type of idea you're working with and how you feel about it.

Would I be satisfied if it turned out I were wrong?
This is a critically important question. Science does not prove positives; the best you can hope for is to gather a mountain of evidence to prop up your idea. It does, however, prove a whole lot of negatives. If you decide to enter your conjecture into the marketplace of scientific ideas, the odds are excellent that it will be partially or wholly disproven, modified, discarded, and/or replaced. At the rate that science has been moving in the last century, the odds are fairly good that this will happen within your lifetime. You should only consider treating your conjecture scientifically if you not only accept but look forward to this eventuality; in science, being "usefully wrong" is an accomplishment that helps humanity move forward in its journey toward understanding the universe more completely.

Can I formulate my conjecture in such a way that it makes measurable predictions?
It's okay to get stuck here for a while. What you're looking for is a formulation along the lines of:

"Under conditions (X, Y, Z...) outcome Q will be detected (more/less) often than would be predicted by (chance/existing theory)."

The "more/less often" part here is important. Your prediction doesn't have to be accurate every single time; it just has to beat the accuracy rate of either pure chance (if there's not currently a theory addressing the situation at hand) or the existing theory.

The observation that helium balloons and hot air rise in the Earth's gravitational field does not invalidate the theory that masses are attracted to other masses; it just means I've failed to identify a confounding variable (the Earth's atmosphere).

The observation that individuals with clearly maladaptive traits occasionally reproduce does not invalidate the theory of evolution by natural selection.

The observation that some years are cooler than previous years, or that some specific regions show a cooling trend, does not invalidate the theory that increased carbon dioxide in the atmosphere leads to increased average global surface temperatures.

If you've conjectured that some people are capable of telepathy, the fact that your telepath occasionally fails to accurately identify what another subject is thinking doesn't necessarily invalidate the whole idea (but you'll have to beat the accuracy rates predicted by both chance and current psychological theories of face/tone of voice reading, possibly by eliminating confounding variables by placing your subjects in different rooms).

As I said, it's fine to get stuck here. It will take some time to figure out what exactly it is that your conjecture might predict, what the current theories in the field are, what they predict, and how your predictions are different. Do be aware that it's perfectly fine (and usually desirable) for your conjecture to predict most or even all of the same things that current theories do, but it does have to set itself apart in some way. If it makes all the same predictions as the existing theory and no new ones, the only ways it can set itself apart are:

1. by uniting and reconciling two conflicting theories (like the Standard Model of particle physics and general relativity). In this case, the theory would in fact make some predictions that differ from those made by each of the existing theories, although it's possible that it would make no new, unique predictions. This is what string theory is trying to do. However, it's struggling to gain acceptance, specifically because it's nearly impossible to validate it as the correct unification because it makes no new, unique predictions. (I'm oversimplifying, but that's the general gist of the problem)
   
2. by being simpler and more elegant than the existing theory, while encompassing all of its predictions. This is, in theory, a nice sort of thing to develop. However, it turns out that when we make theories simpler and more elegant, they often do end up predicting more, because they're more generalized. Newton's laws of motion and universal gravitation were not only simpler, more elegant formulations of Kepler's laws of planetary motion, but also served to predict the motion of objects on Earth. So if you have a conjecture that's simpler and more elegant than the commonly-accepted theory, take a step back from it and look at things it might apply to outside of the realm of the current theory; odds are you'll find it's more general and does in fact make some new predictions.

Can I figure out a way to test my predictions?
This one can be tough too. The real world puts limits on what we can currently test. If the difficulty in testing your conjecture is purely technological - if you can imagine a way to test it if we had infinite energy, better telescopes, better microscopes, better brain imaging, better dating techniques, or fully-equipped zero-g labs - then you've probably got a testable hypothesis, and you should talk to other scientists about how you might be able to test it indirectly. If the difficulty is definitional - if it's built into the definition of your conjecture - then you may have a problem. Specifically, if you're postulating extra dimensions that can't be detected, beings that exist outside the observable universe, extrasensory perception that only works when the subject isn't being observed by scientists, or miracles that happened at some time in the past and left no physical evidence, you're probably dealing with a subject that science isn't equipped to handle.

Now, there are some cases where the difficulty in testing appears to be definitional but is actually technological. If you're predicting the existence of an invisible pink unicorn, it would seem that you'd have a definitional problem - but if your IPU has mass and leaves footprints, or if it's tangible, or if things slow down when they pass through it, and if you have a general idea of where to look for it, then it doesn't matter terribly much that it's invisible except when you're trying to demonstrate that it's pink. This is the case with physicists' search for dark matter, a subject about which we appear to maybe possibly be getting some direct evidence in recent months.

Congratulations! You've got a testable hypothesis!
If you've made it past all those hurdles, your conjecture is now a testable hypothesis. You know the background science, you know what your idea predicts, you know how to test your predictions, and you're ready to go check them against reality! On to Part 3: The Infinite Degrees of Wrong.

Read more!

Nobody really knows what’s going on

Physicists think they might, just maybe, have found some observational evidence here on Earth for the mysterious "dark matter" believed to be responsible for the anomalous behavior of galaxies, and the evidence comes in a form that may provide some support to string theory, a discipline in serious need of some experimental verification. So reports the New York Times. Of course, there's always at least one scientist willing to drop a bucket of cold water over the heads of anybody who gets too excited about the new discovery.

“Nobody really knows what’s going on,” said Gordon Kane, a theorist at the University of Michigan. Physicists caution that there could still be a relatively simple astronomical explanation for the recent observations.

What you can't count on is that the mass media will report those words of caution. But they did this time! It won't prevent the inevitable roar of cheerleading from legions of overexcited amateurs much like myself, but it's a step in the right direction, toward caution in science reporting and a real effort to provide all the different potential interpretations of an incredibly complex issue. It could be a pulsar (really cool) or it could be the elusive dark matter (amazing), or it could be something else entirely. But the main information to take away from the article is that we've discovered something neat, new, different, and special...and nobody really knows what's going on.

The article is excellent. Props to the New York Times. If only all pop-science articles adopted that tone of caution, showcasing a blunt declaration of uncertainty in the second paragraph, we might not have quite so many episodes of "XXX makes you fat/gives you cancer/prevents cancer/kills you/holds the secret of the universe/gives you X-Ray vision!!!" in television news reporting. Of course, that may be giving TV news writers too much credit.

Read more!

Science Basics: How Theories are Made, Part 1

There's a lot of confusion going around when it comes to scientific theories. The very first comment I got on my very first substantive blog entry serves to illustrate that fact. While the folks talking about things like climate change or evolution bear the brunt of the confused people, even such seemingly neutral subjects as particle physics attract people who believe that pseudoscience is somehow morally equivalent to science.

It's therefore necessary, every now and then, to have a basic discussion of what science is and isn't, and specifically what a theory is and isn't. While we all (hopefully) get a basic introduction to the scientific method in grade school, the hypothesis -> experiment -> analysis -> conclusion is a very simplified description of an extremely complex process, one that gets more and more complex as we deal with larger, smaller, or more complex systems.

The Beginning: Conjectures
Most scientific theories are born as conjectures of some sort. A conjecture is, essentially, a guess; it's an exercise in what's called "inductive reasoning," or making a generalization about a process or property based on observation of a specific aspect of it. There are a lot of ways of forming conjectures:

• You can observe an object or event and make a conjecture about its nature, structure, or identity. For instance, I could observe that the moon is pale and lumpy and propose that it is made of green cheese.
  
• You can make a prediction about the behavior of some general class of things, based on the behavior of a single member of that class. For instance, I could observe the behavior of helium balloons and propose that objects are repelled by gravitational fields.
• You can make a prediction based on purely logical or mathematical reasoning from a known theory. For instance, I could propose that all objects in the universe obey Newton's laws of motion.
• You can find an inconsistency in a known theory and postulate an explanation for it. For instance, I could propose that the Arctic ice cap is melting faster than predicted because magma is leaking into the Arctic ocean.
• You can run a computer model or simulation and make a prediction of the behavior of the system it models.
• And there are probably dozens of other ways to come up with your conjecture. There isn't really an invalid way to do this; whatever works for the specific problem you're trying to solve is fine.

The key feature of a conjecture is that it's formulated as a possibility. It may or may not conform to observed reality; it may or may not have any supporting data; it may or may not be contradicted by some existing data. Conjectures are probably the closest thing in science to the meaning of the word "theory" in common speech. If you ever hear the phrase "I have a theory that," chances are you're dealing with a conjecture. UFO claims, predictions based on religious texts, and all the myriad claims of ESP, magic, time travel, extra dimensions, and the like all fall under this umbrella. So do many proposals by scientists, including (at this stage) the mathematical-physics construct called string theory, which is a perfectly good theory in the field of mathematics but rises only to the level of conjecture in the world of science. It's a big umbrella.

Once you've got your conjecture, the first thing you must do is ensure that it conforms with what you have already observed. All of the ones I proposed in the bullet list would fail this test. However, it's not terribly difficult to come up with ideas that might pass it, if you tweak them a little bit.

Next up: Part 2, Hypotheses and Testability.

Read more!

The Reason for Mass: Theory Confirmed!

Physicists ask some very odd questions. It's sort of a longstanding tradition; many of the really interesting discoveries in physical science have been the result of some strange question whose answer seems obvious to most people at the time. The real answer, however, is usually even stranger than the question. The question of what it might be like to travel at the speed of light, for instance, led Einstein to his theories of relativity, which to this day leave most of us with a puzzled feeling as we try to twist our brains in knots in an effort to comprehend it.

They also have a fascination with chopping things up into little tiny bits. We can blame this on the Greeks. Democritus, a fascinating individual, can be credited with the original atomic theory of matter, although it was not until the seventeenth century that this theory began to be accepted and elaborated upon based on observed evidence. Atoms (and their children, molecules) were pretty easy to understand; they were little tiny pieces of known materials. When we chopped up atoms, we got protons, neutrons, and electrons - a little odder, but fairly easily visualized as little spheres creating miniature planetary-system-like objects. The electrons made plenty of sense; they explain electric currents, predict the composition of certain kinds of compounds, and explain certain features of the periodic table. The protons and neutrons fit in with our measurements of atomic masses. So far, so good.

And then it got weird. The masses didn't quite line up; there was some extra mass that couldn't be accounted for using only the masses of the protons and neutrons, and the bigger the atom, the bigger the discrepancy. Some atoms didn't stick together as well as others; they occasionally spat out bits of mass in various ways, in a process known as radioactive decay. Scientists started trying to figure out what made atomic nuclei stick together at all (given that their electromagnetic repulsion ought to make them fly apart), and came up with something called the nuclear "strong force." This implied that there was a whole bunch of energy bound up holding these nuclei together, and that this energy had mass. This was the energy released and the mass lost in radioactive decay and nuclear fission. It was apparently "carried" by a sort of invisible particle called a "gluon." Seriously. Gluon.

And that's where everything came unglued. It turns out the force that holds nuclei together is only a residual effect of the force that holds protons and neutrons themselves together - you see, protons and neutrons are made up of even tinier particles called quarks. And quarks combine in all kinds of different ways besides the well-known protons and neutrons; in fact, there were a bunch of different kinds of quarks besides the ordinary ones in protons and neutrons. There are six different "flavours" of quarks: up, down, top, bottom, strange, and charmed (I told you, physicists are weird!) which combine to make particles. These composite particles were dubbed "bosons." The electron, by the way, is an entirely different sort of animal; it's elementary all by itself, not made up of quarks, and has a whole family of other vaguely-electron-like particles called "leptons." And even worse, all these particles had antiparticles. By the time the current working theory of particle physics, called the Standard Model, was fully-formed, we had a veritable zoo of exotic particles with peculiar names, odd properties, and different masses and behaviors.

This is where physicists started asking the question: Why do these things have the masses they do? The answer seems obvious; stuff has mass because it's made of matter, which has mass because mass is our unit for measuring how much matter we've got. Right? The "why" question seems like circular reasoning. But it's not. The bosons are mostly not exactly made of matter. They're a little bit of matter - the quarks contribute some mass - held together by a lot of energy.

So the "Why do particles have mass?" question is really a two-part problem. The first involves figuring out why quarks themselves have mass; a mechanism for this was postulated in 1963-1964 by several physicists independently, though the theory was eventually named for its last discoverer, a British physicist named Peter Higgs. Essentially, it involves the existence of yet another particle, this one responsible for creating a field which endows other particles with mass as they move through it. This particle has yet to be detected, apparently because it's really big by particle standards (paradoxically, being big makes particles harder to find); it's one of the main things the Large Hadron Collider at CERN in Switzerland is looking for. You may have seen this on the news recently, since it just came on line this fall.

The second part, however, accounts for the vast majority of the mass of bosons: the energy involved in "gluing" them together. And that is the real subject of today's entry. It appears that the theory was correct - the energy of the interactions between quarks and gluons is enough to account for 95% of the mass of protons and neutrons! (remember that we've already established that energy is mass). It gets a lot weirder than I've described here, what with the gluons popping in and out of existence and changing the colour of quarks. I'm not going to get into quark colours; flavours are enough for one day. But check the article out at Discover Magazine! This is really a big deal; we've made a real, significant advancement in particle physics, and it didn't even involve expanding the particle zoo!

Read more!

Hello, world?

Greetings! Welcome to Even More Grumbine Science! This is my first foray into the blogosphere as an independent blogger, so it may take me a little while to get used to the medium, but I hope you'll enjoy reading it anyway.

I expect to mostly be discussing science, with a general focus on physics and related origin-of-life-the-universe-and-everything fields, from the perspective of an undergraduate student and generally-interested layperson. I don't expect to be discussing anything terribly technical, since I don't yet know very much in that department, but please do not hesitate to ask for clarification if necessary. On a related note, please correct me when I am wrong; as I said, I am only a student.

To those who may be wondering about the name of the blog: It's the newest member of a family of blogs. The others are by my father and his sister. The first is of interest to anyone looking for general information on what science is and how to do it, with an emphasis on climatology and glaciology. The second is specialized information for my aunt's middle-level science classes. While I don't necessarily expect that a large amount of traffic will migrate all the way over here from there, I would like to welcome any young students who do end up here; please feel free to browse around, and if you find anything confusing (or particularly interesting) leave a comment!

Because there's a slight chance some young people could end up here, comments will be lightly moderated to ensure that language and topics of discussion are reasonably appropriate.

Thanks for visiting!
Read more!